Equilibria | Dynamic Sorption, Breakthrough Curve Measurement, mixSorb, dynaSorb BT

Determination of mixture adsorption equilibrium data from breakthrough curves

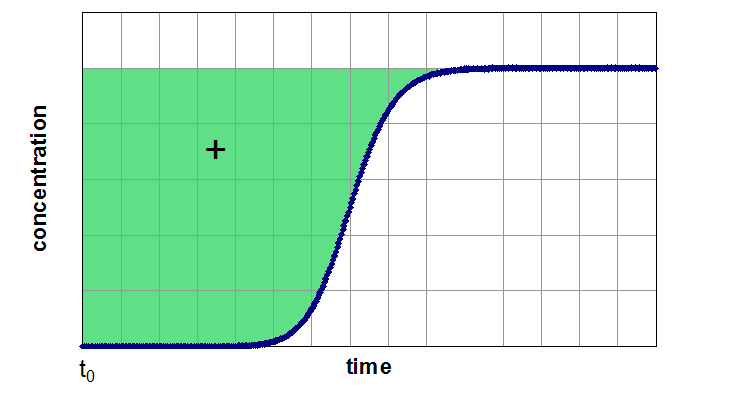
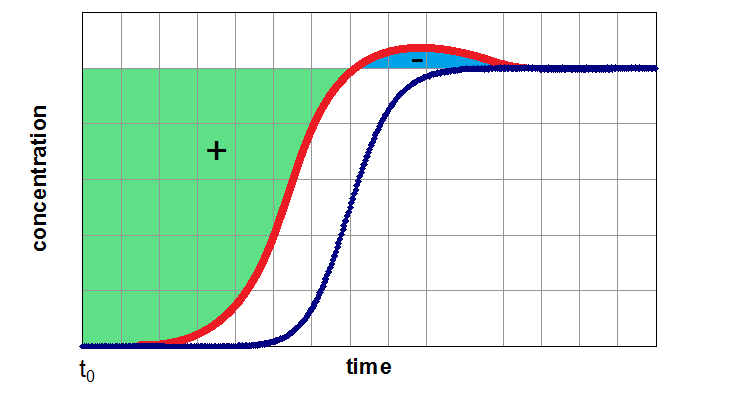
If the adsorber is fully equilibrated (segment 3 of the breakthrough curve), one can determine the equilibrium loading of the examined component by integration of the area above the curve. In next figure, this method of evaluation is shown for a breakthrough of a single component (left side) from a carrier gas and for a breakthrough of a mixture of two components (right side). Depending of the assumption of a non-adsorbable carrier gas the figures are related to pure adsorption equilibria (left side) and binary equilibria (right side). If the carrier gas is a further adsorptive (adsorbable carrier gas), the left side results in a partial loading for a binary mixture and the right side for partial loading values for a ternary mixture.

Integration area for a simple breakthrough curve

Intergation area of the weaker adsorbed component, the blue labeled area of the roll-up effect have to be subtracted.

Integration area of the weaker adsorbed component, the blue labeled area of the roll-up effect have to be subtracted.

Mixture Adsorption Data from a Breakthrough Curve

In general, the dynamic method is suitable to investigate competitive adsorption. With this technique the user can determine mixture sorption equilibria by applying two different options.

the carrier gas is adsorptive 1 (usually the less adsorbed component) and the adsorber will pre-loaded with this component. Afterwards the adsorptive 2 will be additionally dosed into the adsorber. As a result a simple breakthrough curve of adsorptive 2 will be expected. By evaluation of this curve related to the equilibrium loading, the partial loading of compontent 2 can be determined (left side of figure above).
the carrier gas is assumed as non-adsorbable (i.e. He) and the gas mixture of adsorptive 1 and adsorptive 2 will be dosed simultaneous. For this more complicated case the result seems similar to the right side of the figure above). By integration of both curves both partial equilibria can be determined. The sum of both values will give the total value for the investigated binary mixture.

The yielded mixture data are helpful to verify predictions of mixture behavoir by thermodynamic models. Such predictions can be achieved from pure gas isotherms by multicomponent approaches, i.e. by Multi Component Languir isotherms or by Ideal Adsorbed Solution Theory.

Evaluation of a Breakthrough Curve

From the highlighted area the total amount of the adsorbed species is given by:

Equation1: Adsorbed Amount is the integrated ingoing molar flux minus the integrated outgoing molar flux

If the ideal gas law is applied, the molar flow rates can be expressed by volumetric flow rates and the volume fractions.

$Equation2: Adsorbed Amount is the integrated (ingoing Flow rate over molar Volume times the incoming Volume Fraction) time minus (the integrated outgoing volume fraction over time times the outgoing flow rate over the molar volume)$

In these equations all physical variables subscribed with “in” correspond to the conditions at the adsorber inlet. All indicated variables with “out” are quantities for the adsorber outlet. In most cases the adsorptive concentration and inlet volume flow is kept constant during the whole experiment. Therefore the equation can be simplified to:

$Equation3: Adsorbed Amount is the ingoing Flow rate over molar Volume times the incoming Volume Fraction times time minus (the integrated outgoing volume fraction over time times the outgoing flow rate over the molar volume)$

For high diluted systems the outgoing volume flow rate can be considered as constant and equal to the value of inlet volumetric flow rate of the adsorber (neglecting the adsorptive volume). Then the equation is furthermore simplified to:

$Equation4: Adsorbed Amount is Flow rate over molar Volume times (the incoming Volume Fraction times time minus the integrated outgoing volume fraction over time)$

The equations show that the molar flux of the adsorptive is the product of the outgoing volumetric flow rate and the outgoing volume fraction. Therefore, an error for the assumption of a constant volume flow during the whole bed is only present for the second segment – the mass transfer zone – since in the first segment the volume fraction is zero and in the third segment the assumption of inlet volumetric flow rate being equal to outlet volumetric flow rate is valid.

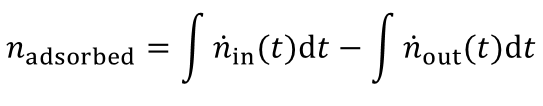
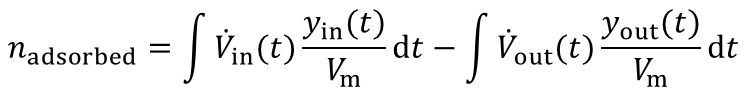
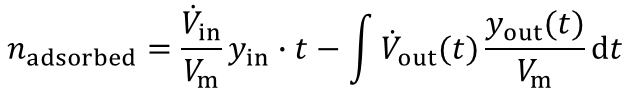
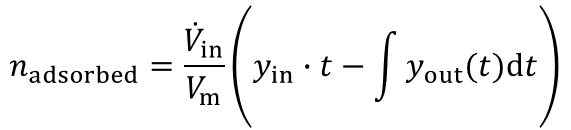
In most industrial applications impurities are present at very low concentrations (i.e. CO₂ removal from air, removal of toxic impurities from waste air, compliance of air-pollution law). Here a competitive adsorption of the main components can not be neclected. Furthermore the equation above is valid for such high dilutions. An evaluation of a breakthrough curve is therefore easily possible. Based on this considerations the dynamic method is the best choice to investigate the suitability of adsorbents for separation of impurities in highly diluted systems.

Mixture adsorption equilibria are easily accessible by the dynamic method. An automatic measurement of a mixture gas adsorption isotherm with variable partial pressures and a constant total pressure is possible. For high diluted mixtures the dynamic method would be the best choice.

Continue reading - Kinetics...